Facial Recognition System Using CNN
Overview
For this project, a partner and I designed and implemented a facial recognition software. For the sake of comparison, we decided to design and implement two competing architectures, each utilizing a different loss method for the neural network. The cross-entropy and triplet loss methods were compared for performance and scalability. The triplet loss method was chosen due to it's flexibility in adjusting to larger datasets and popularity in industry.
Our Approach
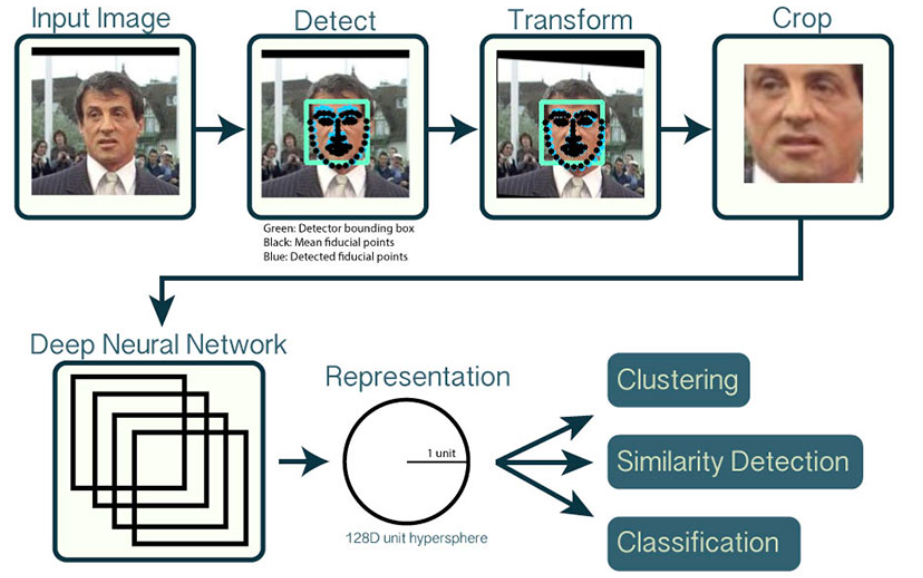
The data flow of the system can be described as follows. First, an image is chosen for analysis with a visible face, or faces. The software then detects every visible face in the image. Each face is transformed to a fixed size and dimension so that every face is identical in size. If the face is rotated in the image, it is transformed such that the detected eyes lie parallel and are vertically centered in the frame. This step is important to maintain continuity when measuring and comparing faces. Next, the transformed face is cropped and passed through the convolutional neural network. For the cross-entropy model, the network will output an array of probabilities that the input image is most similar to each class. In the case of the triplet loss model, each class will be assigned 128-d vector encoding. These vectors are based on measurements taken between key facial features. Finally, each face is classified based on the previously assigned vectors. If the feature vectors of the face are within a certain threshold of similarity to one of the faces in our dataset, the classifier matches the names and will output the person's name accompanied by the percentage confidence of that determination
Data & Methods
Like many computer vision applications, face recognition presents a problem that can be tackled with a wide range of varying approaches. Existing strategies range in complexity and difficulty. The LFW, or “Labeled faces in the Wild” database, provides thousands of images of people with labeled faces (Face Recognition, 2020). This database was used for the testing and training of our neural network. Two different loss models were tested for this project in order to compare performance and achieve the highest possible accuracy. Each model was accompanied by a different neural network. For the cross-entropy loss model, the neural network was a 7-layer convolutional neural network. The triplet loss method was also implemented and this was accompanied by a 5-layer convolutional neural network.

Our first approach implemented a sparse categorical cross-entropy loss function with a softmax activation. This model returns a multinomial probability distribution applying to all classes in the provided dataset (Brownlee, 2020). This method had plenty of documentation and was quite simple to implement and test and is typically quite accurate for datasets with a manageable number of classes. After countless design iterations we achieved the best testing accuracy at 85.76%. Our final model consisted of seven convolutional layers with four applications of max pooling and periodic batch normalization and dropout functions to reduce overfitting. The issue that was found with the softmax method is the lack of flexibility and the significant decrease in accuracy when dealing with larger datasets.
The second approach employed a semi-hard triplet loss function to learn good embeddings for the images. This method was considerably more difficult to implement. Despite tensorflow having a triplet loss function included in its framework, the amount of helpful documentation was limited. The triplet loss method allows for variable numbers of classes. This allowed for more faces to be enrolled in the database while still maintaining high accuracy. Triplet loss uses an anchor photo for each class which is compared to other photos. A positive match is added to the same class as the anchor photo and a negative is placed in a different class (Moindrot, 2018). This process is all done automatically via online triplet mining performed by the adapted TensorFlow functions.
Evaluation
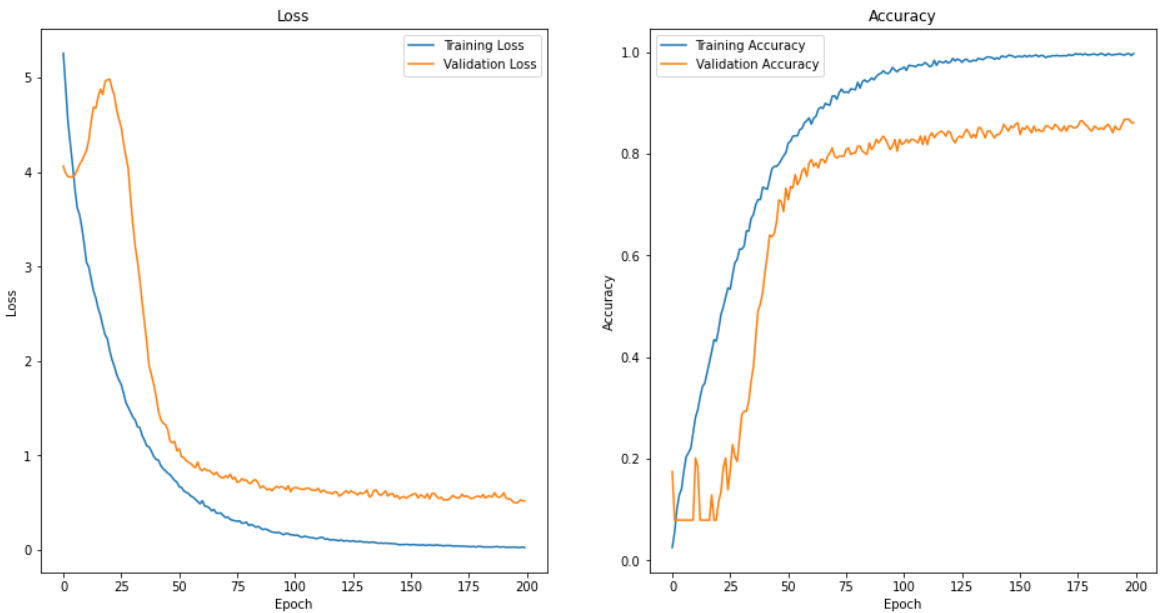
The evaluation of our project is concerned with the accuracy of our recognition software and the performance difference between the CNN models. We tested the system by splitting a large open-source database of labeled faces into training, testing, and validation datasets with an equal distribution of classes in each. To properly prepare the LFW database for evaluation, we eliminated all classes (or people) from the dataset that had less than 15 face images associated with them. This left us with approximately 3000 images and 62 classes to train and test with. This made it simple to find the accuracy of the implemented systems. For the cross-entropy model the testing was relatively easy. Since each face in the testing database is labeled, we were able to pass many images through and compare the result with the actual result until a concrete number for accuracy was reached. The training versus validation loss and accuacy is shown below.
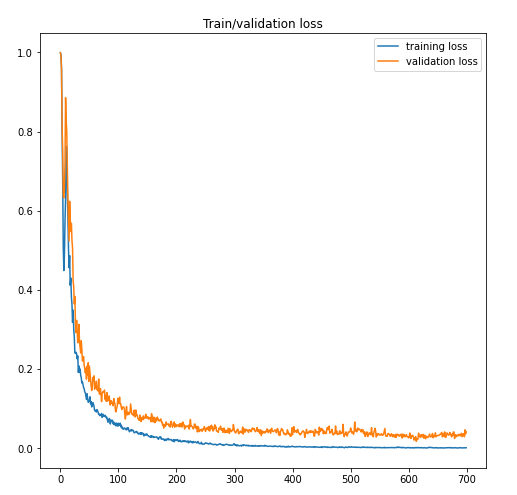
Evaluation for the triplet-loss function required a few more steps. First, the model was trained using the semi-hard triplet loss function adapted from TensorFlow. Next, we transformed the encodings of each trained image into a 2-d array and plotted them to track the development of the cluster formations. The encodings were then averaged for each class and added to a dictionary to act as the anchor embedding for each particular class. A k-nearest-neighbor classifier was used to predict images from the testing dataset. The accuracy was then determined by manually dividing the number of correct results by the length of the test set. The training versus validation loss is shown below.
Results
As discussed earlier, our first approach employed the use of a categorical cross-entropy loss function. Our final design iteration for this method achieved a high accuracy of 85.76%. The design process for this particular model consisted of altering the shape of the neural network, the number of epochs, and the learning rate. In terms of the shape of the neural network we tried all kinds of combinations for the number and size of convolutional layers and played around with batch normalization and dropout to deal with overfitting. The neural network was trained after each design iteration and changes were made based on the trend of the validation and training loss and accuracy, as shown above. Our final design consisted of 7 convolutional layers with 4 max pooling layers interspersed between to reduce dimensionality. Every pooling layer was followed by batch normalization and dropout to mitigate overfitting of the results. These layers were followed by two dense layers and a final layer with softmax activation.
The evaluation of the triplet-loss model was slightly different than that of the cross-entropy. Our final triplet-loss model achieved an impressive accuracy of 79.1%. Albeit lower than the categorical cross-entropy model, this architecture has proven in literature to be far more scalable datasets with more classes. In addition to raw statistics, the performance of this method can be visualized through Principal Component Analysis (PCA). The plot below illustrates the distribution of embeddings created for faces. As you can see, there is a clear difference in cluster distribution before and after applying semi-hard triplet loss. Each point represents a face and each color represents a different person or class.
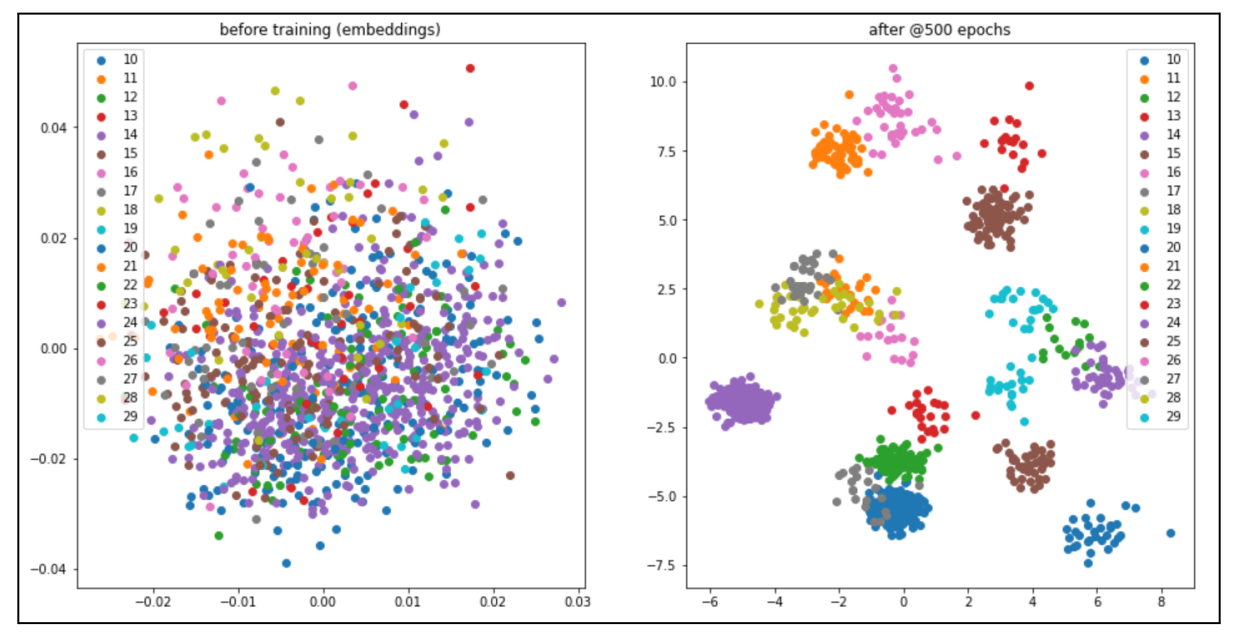
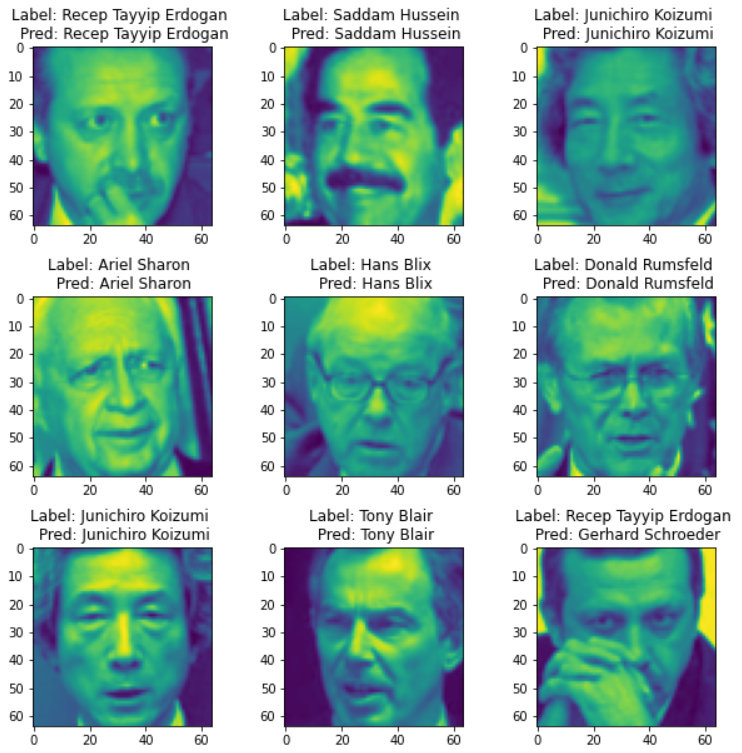
As you can see, there is a clear difference in cluster distribution before and after applying semi-hard triplet loss. Before training, the image encodings appear random with no observable pattern. Contrarily, after applying 500 epochs of semi-hard triplet loss, the embeddings for each image have been clearly grouped together by class. Admittedly, there are still significant overlaps between classes which can be attributed to our less than perfect design. We did our best to mitigate this effect by using a K-neighbors classifier for the predictor but some of these are hard to avoid. That being said, these results were very exciting to see as our first few iterations were not nearly as accurate. To reach the final design iteration we followed a similar process to the cross-entropy model by altering and testing different components of the network. Below is an example of the predicted values compared with the actual identity.